相互作用
右図は,グライダーをセルオートマトンにより動かしたものです.初期状態から状態遷移を繰り返すと,グライダーは左下に進みす.左下にあるブロックとぶつかり粉々になり,最後は両者とも消滅します.簡単なプログラムですが,時間の変化とともにまるで生き物のような動きをします.
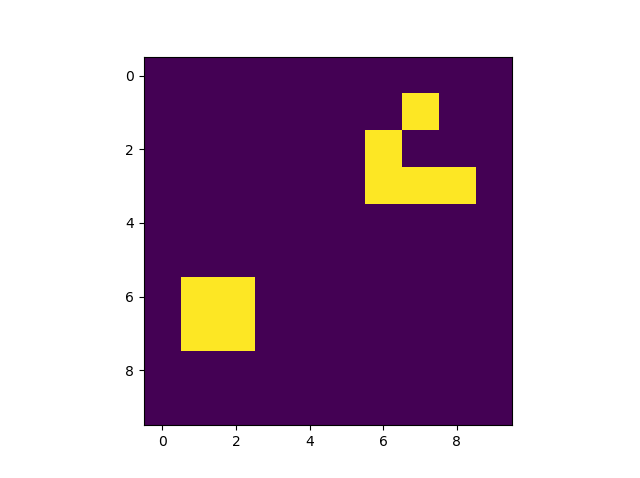
グライダー(初期状態)
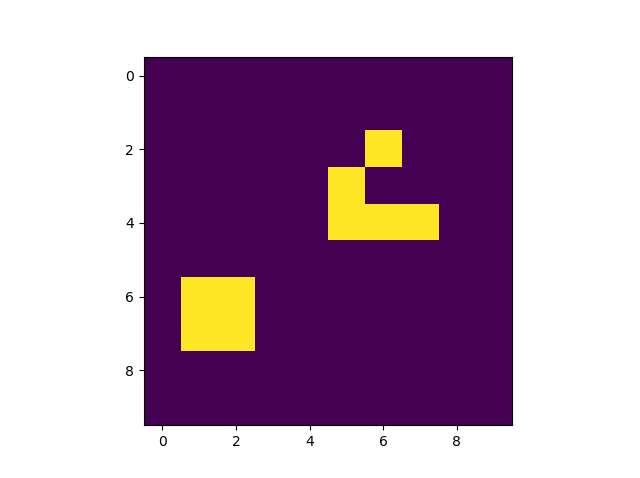
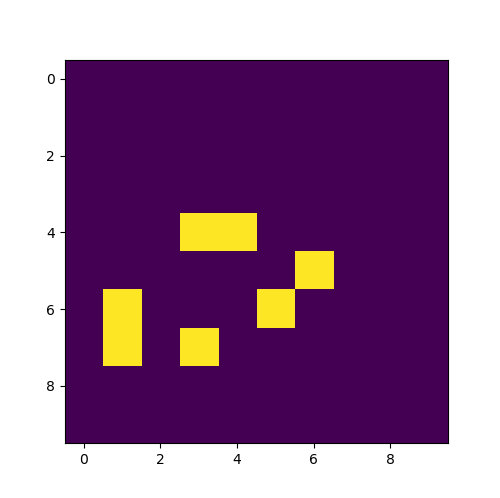
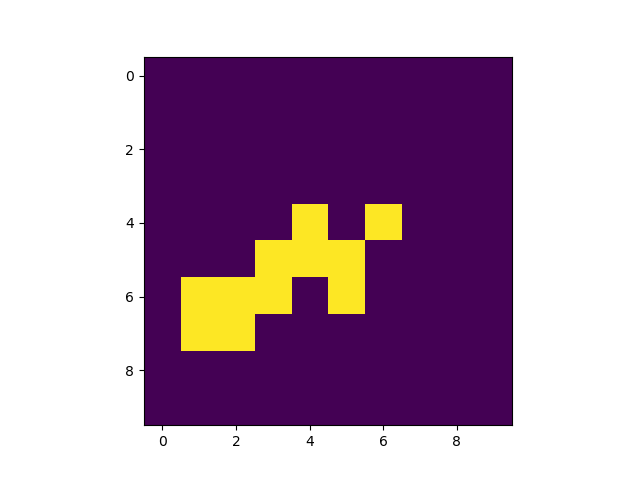
4回目 | 9回目
10回目 | 14回目
セルオートマトンのpythonプログラム
(使用のときは段落等を揃えてください.ズレるかも…)
import cv2
import matplotlib.pyplot as plt
def calcnext(x,y):
no=0
for j in range(y-1,y+2):
for i in range(x-1,x+2):
no += w[i][j]
no -= w[x][y]
if no == 3:
return 1
elif no==2:
return w[x][y]
return 0
def nextt():
n=[[0 for i in range(10)] for j in range(10)]
for y in range(1,9):
for x in range(1, 9):
n[x][y]=calcnext(x,y)
for y in range(10):
for x in range(10):
w[x][y]=n[x][y]
def main():
img=cv2.imread("test.txt") ← 初期状態をtextで与えています.
data=cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
global w #グローバル
w=[[0 for i in range(10)] for j in range(10)] #配列用意
w=data #代入
for i in range(0,55):
nextt()
plt.imshow(w)
plt.pause(.01)
if __name__ =="__main__":
main()
また,セルオートマトンは幾何学的な模様を作成したりします.
相互作用や自己組織化について
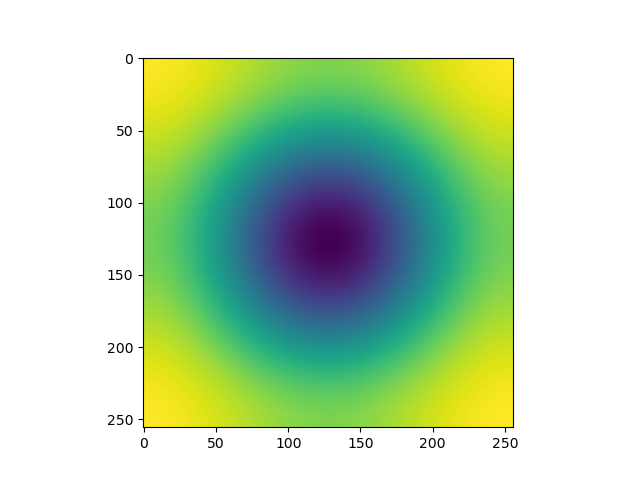
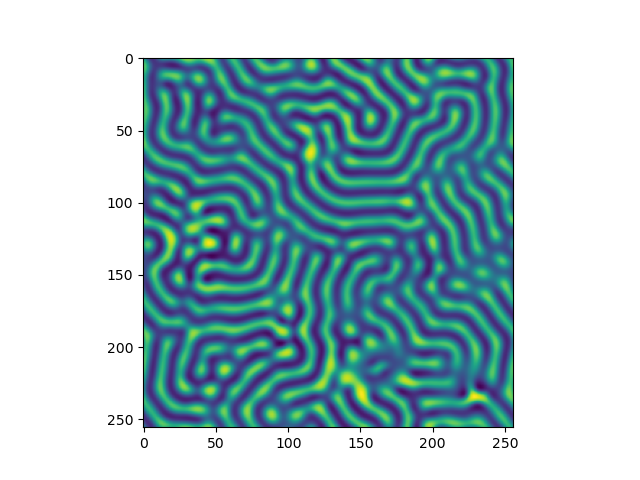
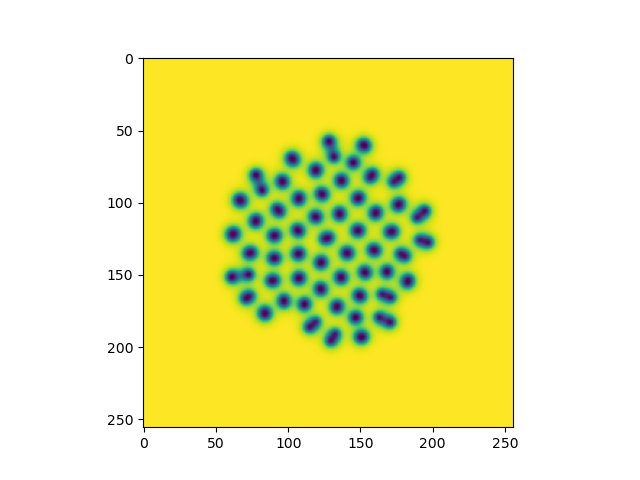
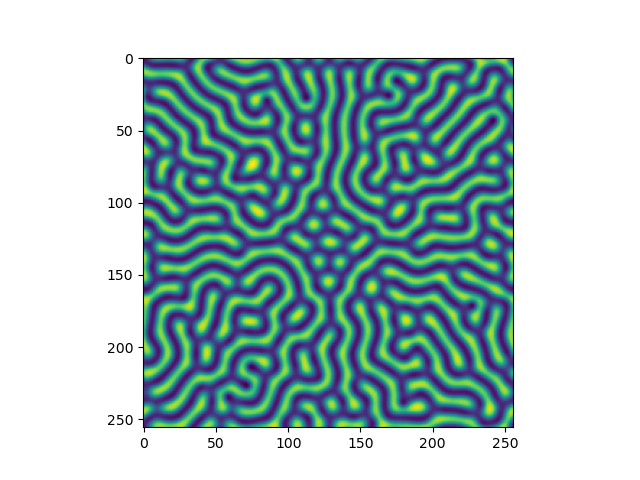
上のセルオートマトンも近傍画素との相互作用でしたが,右の縦4つの図は,反応拡散方程式によりチューリングパターンを作成したものです.反応拡散方程式の数式は関連する本を見て頂けばわかりますので割愛しますが,拡散方程式に反応項が加算されています.拡散速度と反応速度の異なる2つの物質が相互作用し,自発的に組織化されこのような模様を作ります.このようなパターン形成にはリズムとフィードバックが重要であり,周期的な波を作るためには,2階の微分方程式を含む必要があります(他にも手はありますが^^;).非平衡(バランスが崩れている)と非線形の中の秩序がこのような現象を起こします.生物の模様,心臓のリズム,呼吸のリズム,ケガの回復など,我々の身の回りには自己組織化(秩序)が起きています.これらのリズムは多少ズレても,リミットサイクルと呼ばれる引き込み現象により安定に戻ります.この自己組織化はニューラルネットワークの学習にも関係しています.
右縦図(グレイ・スコットモデルより)の一番上は,拡散方程式のみの状態変化を表しますが,下図3つ(順にstripe,spot,amorphous)は同じ数式(拡散方程式に反応項を加算した式)であっても,時間が経過すると,拡散と反応の濃度変化の違いから異なった形に組織化されます.確かに生物の模様に似ていますね,やはりチューリングは天才ですね(・_・;)).pythonプログラムを一部抜粋しておきます.
dudt = Du*laplacian_u - u*v*v + f*(1.0-u)
dvdt = Dv*laplacian_v + u*v*v - (f+k)*v
u += dt*dudt
v += dt*dvdt
plt.imshow(u) # uの表示
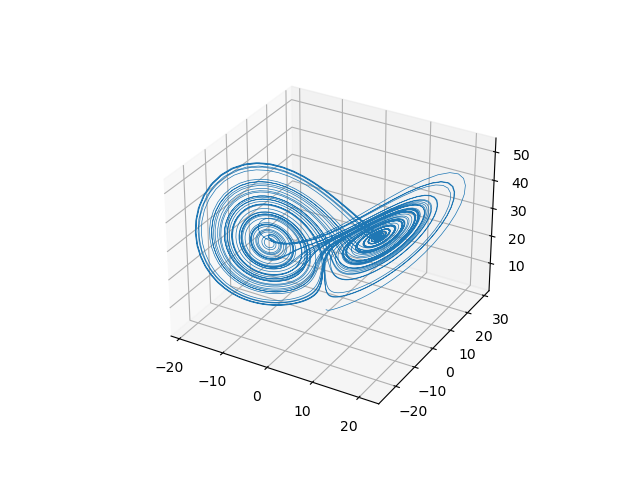
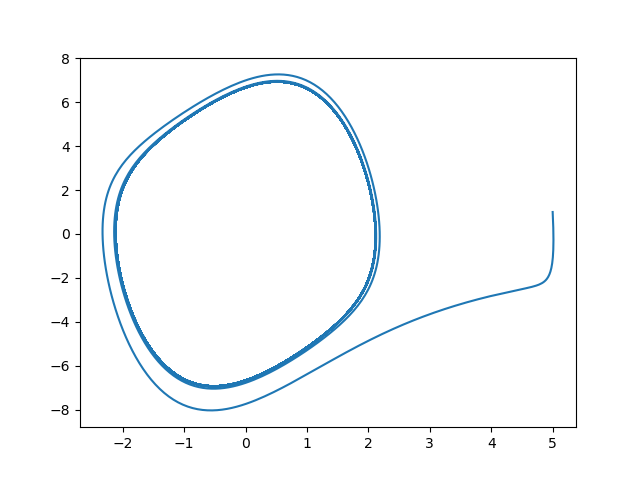
また,相互作用や複雑系とパターン形成などについて考えています(下図左:ローレンツアトラクタ,右:リミットサイクル).心臓にもカオスの要素があるため,多少不規則な動きをしても,引き込み現象が起こり安定状態に戻ると考えられます.このような相互作用の画像への応用を考えています.
例えば,自ら構造を形成する機能を持つ集団に,原子核の連鎖反応があります. この原子核反応も拡散と反応からなる反応拡散方程式と捉えることもできます.平衡のように時間変化が0のとき,ある物理量(粒子密度の定常分布など)のラプラシアン∆は拡散方程式になります(そこに反応項を加えます).最初にわずかなゆらぎがあると,ある物理量から出て来た固有値側で連鎖反応が爆発的に起こります.このような自発的な構造の発生は,固有値をパラメータとした分岐現象と捉えることができそうです.その構造が固有値よって決まることになります.
その他にも,ディジタル化画像でサンプリング不十分な場合に見られるモアレ像も,物理的に波どうしの合成作用で”うなり”として捉えることもでき,幾何学的な模様を作ります(キーワード:エリアシングエラー).
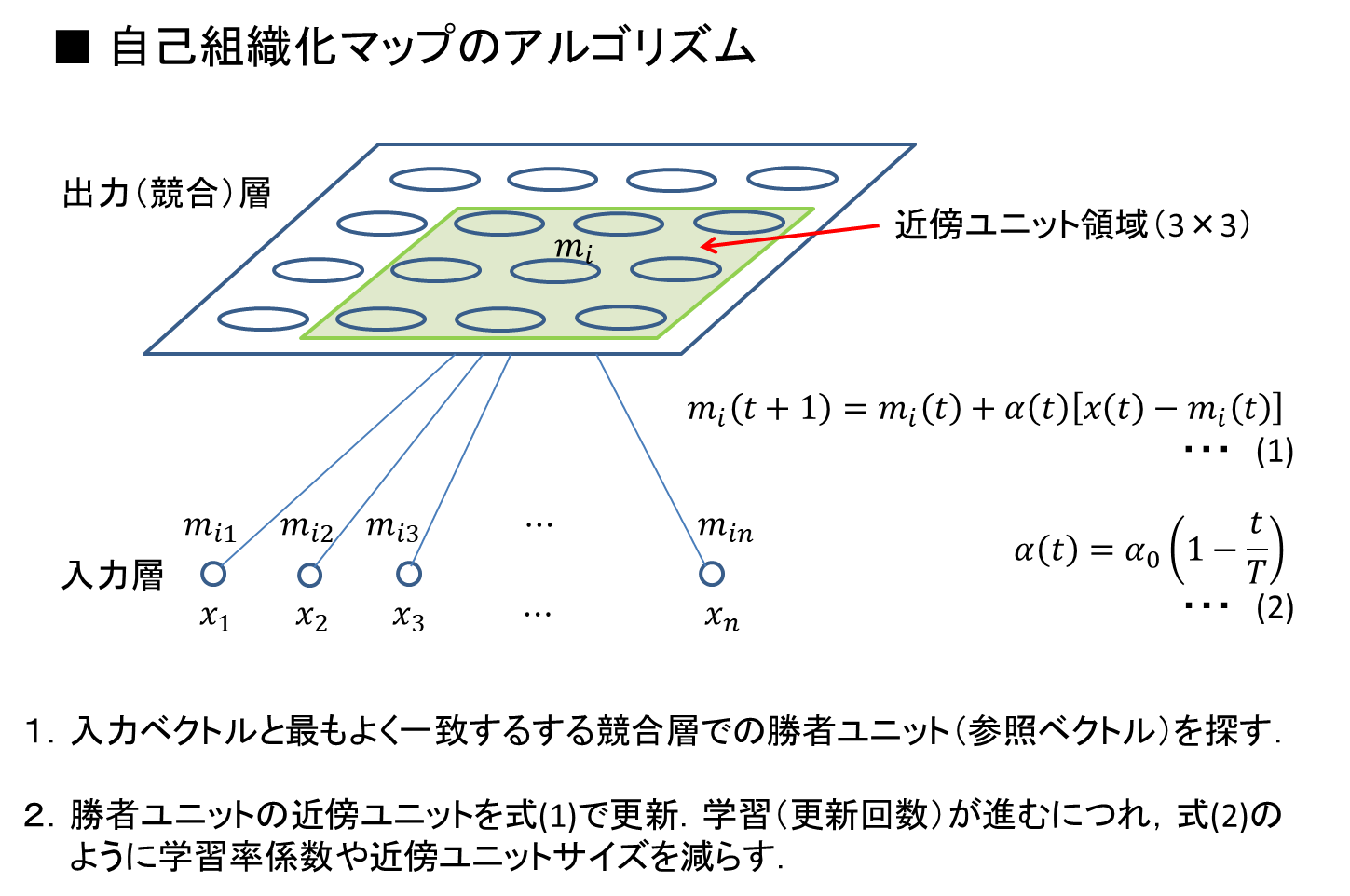
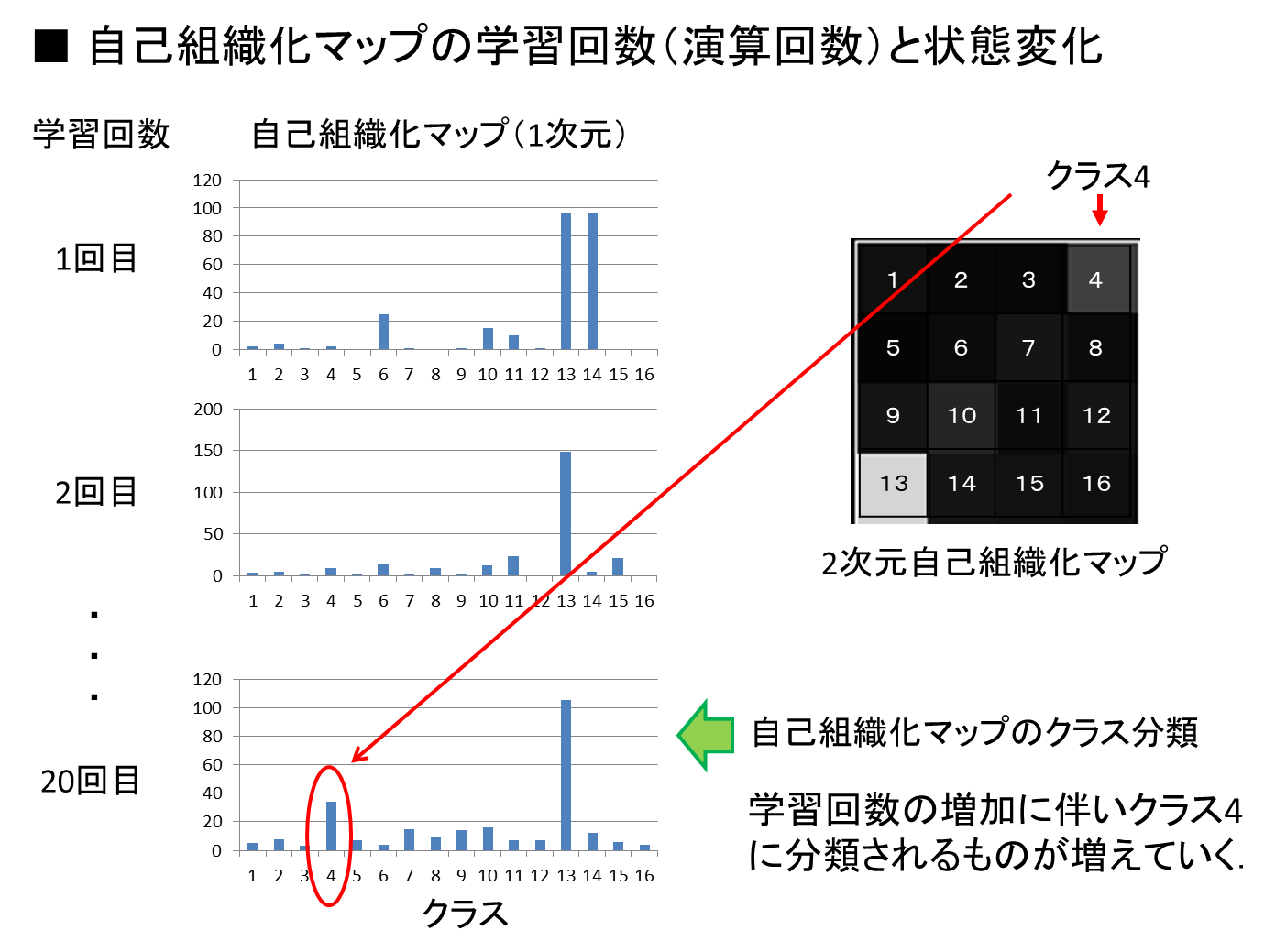
教師なし学習の一つである,自己組織化による競合や協調を用いたクラスタリング,相互作用による秩序形成の研究をしています.
自己組織化システムの数学的な基礎についてはここでは省略しますが,線形・非線形系の状態変化であるダイナミクスを捉えることが大事です.上図は,あるデータに関してKohonenによる自己組織化マップを適用したものです.この自己組織化マップは,入力パターンとネットワーク内に蓄積されたベクトルとの比較を繰り返すことで,自己組織化(自発的に組織化)されます(上左図).具体的には,入力データがユニットのもつベクトルに適合したとき,そのユニットの近傍領域がクラスの学習データの平均を表現するように最適化(重みの修正を学習)されます.結局,無秩序であったユニットの組みが,局所表現として特徴マップに収束し,自己組織化されることになります(上右図).通常,高次元のデータをもう少し大きなマップに写像するため,各クラスは領域として選択されますが,ここでは頻度を利用しています.
線形ベクトル場や非線形ベクトル場を理解することが分岐理論へと繋がっていきます.線形系では自発的なパターン形成は難しい(出力がぼけること・独立であること)ですが,上の例ような非線形系では,自発的にパターンを形成するような複雑なこと(相互作用)が起こります.このようなところに何らかの「秩序」が出現してきます(パターン形成に登場する式は複雑ですが,拡散項を除いた場合の二次元力学系の振る舞いによりTuring系,振動系,興奮系,双安定系の4つのクラスに分けられます.初めの3つはアトラクタが1つですが,双安定系には2つあります).結局,自己組織化とは自発的に自己秩序化されることになりますね.このようなパターン形成の仕組みがわかれば目的対象物を捉えやすいのではないかと考えています.
強化学習
シングルエージェントによる強化学習を用いた研究をしています.
https://www.tandfonline.com/doi/full/10.1080/13102818.2024.2338433?src=exp-la
エージェントは環境間との相互作用をもとに報酬を得ていますが,マルチエージェント化することで更なる相互作用の発現を期待しています.行動学習から進化へと繋がります.